写这篇文章始于在开发中解决这个问题：

pub struct StringDt{
    pub value: Option<String>,
    pub extension: Option<Vec<Extension>>,
}

规则是value和extension取值不能全部为空，但是也不能同时存在。看到这种规则，第一时间想到的就是逻辑异或操作。

value.empty() ^ extension.empty()

解决完问题后，觉得以前XOR这些逻辑运算规则都是靠强记的。然后在网上查了一些资料，看看有没有更生动形象的解释能够帮助理解记忆，于是有了这篇文章。

官方定义

异或运算是一种数学运算符，主要应用于逻辑运算和计算机体系中的位运算。XOR 全称为exclusive OR，中文称为异或运算。

异或运算的数学符号常表示为“⊕” ，有着如下的运算规则：

• 0 ⊕ 0 = 0 （0与0异或运算的结果为0）
• 0 ⊕ 1 = 1 （0与1异或运算的结果为1）
• 1 ⊕ 0 = 1 （1与0异或运算的结果为1）
• 1 ⊕ 1 = 0 （1与1异或运算的结果为0）

解释

正统的解释：不进位加法

异或也叫半加运算，其运算法则相当于不带进位的二进制加法：二进制下用1表示真，0表示假，则异或的运算法则为：0⊕0=0，1⊕0=1，0⊕1=1，1⊕1=0（同为0，异为1），这些法则与加法是相同的，只是不带进位，所以异或常被认作不进位加法。

更形象的解释：翻牌

异或运算可以类比于翻牌处理。

我们对扑克牌进行翻转|不翻转处理，发现结果和异或运算是一致的。

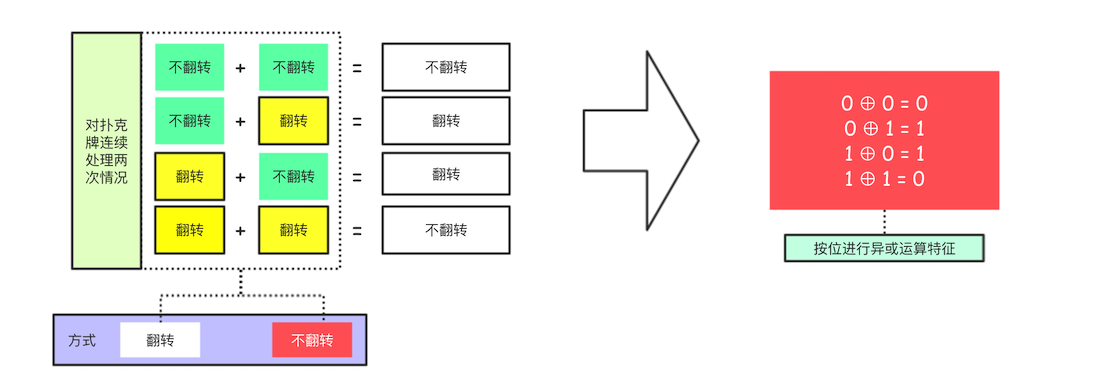
最主要的应用：密码

现在我们已经清楚了异或运算的特点，下面来看看怎么利用异或操作来进行加密：

上面的图形展示中，我们把实心点设为1，空心点设为0，那么第一张图相当于原文，第二张图作为蒙版（相当于密钥），盖在第一张图上，可以得到第三张图（相当于密文）。这个过程是可逆的，如果把第二张图继续当作蒙版，盖在第三张图上，那么将能还原得到第一张图。

但是我们很少完全用异或进行加密

其实像上面的这种处理方式在1917年就由维纳（G·S Vernam）提出，并获得了专利，被称为一次性密码本（One Time Pad），也被称为维纳密码（Vernam cipher)。

香农（C.E.Shannon)在1949年用数学证明：

一次性密码本是无条件安全的，理论上是无法破译的。

那为何很少有人使用一次性密码本呢？原因有以下几点：

• 密钥配送问题
  • 最大的问题在于密匙的配送！当B收到了来自A的密文，想要解密时，就必须知道密钥，因此密钥也应该配送过去，且密钥的长度和密文相等。但这产生了一个矛盾-------如果能够安全的发送密钥，难道不能安全的发送明文吗？
• 密钥的保存
  • 如果有能力安全保护密钥的方法，不就能安全的保护明文了吗？也就是说，一开始我们就不需要密码。
• 密钥的重用
  • 在一次性密码本中，绝不能重用过去用过的密钥，否则密钥一旦泄露，过去所有的机密通信将全部被解密。
• 密钥的同步
  • 当密文很长时，一次性密码本的密钥长度也会随之变长。明文为1G的大小，则密钥的大小也为1G。
• 密钥的生成
  • 在一次性密码本中，需要生成大量的随机数。这里的随机数不是通过计算机生成的[[伪随机数]]，而必须是无重现性的真正的[[随机数]]。

不过，虽然直接应用XOR运算的可逆性实现的一次性密码算法无法在商业中真正应用，但我们还是能在很多经典的加密算法（比如，DES和AES）中看到XOR运算的身影。

最后的话

又回到最开始的那个实际问题，当我认为我给出了最佳的处理方法后，我发现了这段代码：

value.empty() != extension.enpty()

呵呵！我也不知道哪个是最佳的了！！！

References

• 异或运算（XOR）[通俗易懂]，腾讯云，开发者社区，2022-09-07